KDL wiki
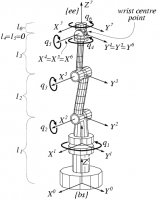 Kinematic Chain
Kinematic Chain
Skeleton of a serial robot arm with six revolute joints. This is one example of a kinematic structure, reducing the motion modelling and specification to a geometric problem of relative motion of reference frames. The Kinematics and Dynamics Library (KDL) develops an application independent framework for modelling and computation of kinematic chains, such as robots, biomechanical human models, computer-animated figures, machine tools, etc. It provides class libraries for geometrical objects (point, frame, line,... ), kinematic chains of various families (serial, humanoid, parallel, mobile,... ), and their motion specification and interpolation.
Installation Manual
This document is not ready yet, but it's a wiki page so feel free to contribute
Requirements
Supported Platforms
- Linux
- Windows
- Mac
Installation
There are different ways for getting the software.
From debian/ubuntu packages
Orocos KDL is part of the geometry stack in the ROS distributions pre-Electric.
- ros-cturtle/diamondback-geometry
Since ROS Electric it is available stand-alone as the orocos-kinematics-dynamics stack.
- ros-electric/fuerte-orocos-kinematics-dynamics
Source using git
git clone https://github.com/orocos/orocos_kinematics_dynamics.git
Building source with ROS
- Follow the guidelines at Building ROS packages to build orocos_kdl with catkin_make_isolated
Building source with plain CMake
- goto your orocos_kdl directory
- create a build directory inside the orocos_kdl-dir and go inside:
mkdir <kdl-dir>/build ; cd <kdl-dir>/build
- Launch ccmake
ccmake ..
- configure [c], select the bindings you want to create, choose an appropriate installation directory
- configure[c], generate makefiles [g]
- make, wait, install and check
make;make check;make install
KDL typekit
The use of KDL types in the TaskBrowser
Compiling
You need to check out the rtt_geometry stack which contains the kdl_typekit package here:http://github.com/orocos-toolchain/rtt_geometryand build&install it using the provided Makefile (uses defaults) or CMakeLists.txt (if you want to modify paths).
Importing
Import the kdl_typekit in Orocos by using the 'import' Deployment command in the TaskBrowser or the 'Import' Deployment property in your deployment xml file:
import("kdl_typekit")
Creation of variables of a KDL type
- Make sure you've loaded the KDL typekit, by checking all available types in the TaskBrowser:
.types
- In the list you should find eg. KDL.Frame, so you can create a variable z of this type by:
var KDL.Frame z - z has a standard value now (Identity frame), there are multiple ways to change it:
- value by value:
z.p.X=1orz.M.X_x=2
- the full position vector
z.p = KDL.Vector(1,2,3)
- the full rotation matrix
z.M=KDL.Rotation(0,1.57,0)(roll, pitch, yaw angles???)
- You can check the current value by just typing it's variable name, for this example, z.
z
- Look in the KDL typekit for more details
User Manual
Why to use KDL?
- Extensive support for :
- Geometric primitives: point, frame, twist ...
- Kinematic Trees: chain and tree structures. In literature, multiple definitions exist for a kinematic structure: a chain as the equivalent for all types of kinematic structures (chain, tree, graph) or chain as the serial version of a kinematic structure. KDL uses the last, or using graph-theory terminology:
- A closed-loop mechanism is a graph,
- an open-loop mechanism is a tree, and
- an unbranched tree is a chain.
- Next to kinematics, also parameters for dynamics are included (inertia...)
- Kinematic and Dynamic Solvers: various generic forward and inverse kinematic algorithms, redundancy resolution, ...
- Instantaneous Motions: under construction (Expected release, Spring 2011)
- Motion Trajectories: Cartesian paths, velocity profiles, Cartesian trajectories
- Realtime-safe operations/functions whenever relevant: they do not lead to dynamic memory allocations and all of them are deterministic in time.
- Python bindings
- Typekits and transport-kits for Orocos/RTT
- Integrated in ROS
Getting Help
Geometric primitives
KDL::Vector
A Vector is a 3x1 matrix containing X-Y-Z coordinate values. It is used for representing: 3D position of a point wrt a reference frame, rotational and translational part of a 6D motion or force entity : <equation id="vector">$\textrm{KDL::Vector} = \left[ \begin{array}{ccc} x \\ y \\ z \end{array}\right]$<equation>
Creating Vectors
Vector v1; //The default constructor, X-Y-Z are initialized to zero Vector v2(x,y,z); //X-Y-Z are initialized with the given values Vector v3(v2); //The copy constructor Vector v4 = Vector::Zero(); //All values are set to zero
Get/Set individual elements
The operators [ ] and ( ) use indices from 0..2, index checking is enabled/disabled by the DEBUG/NDEBUG definitions:
v1[0]=v2[1];//copy y value of v2 to x value of v1 v2(1)=v3(3);//copy z value of v3 to y value of v2 v3.x( v4.y() );//copy y value of v4 to x value of v3
Multiply/Divide with a scalar
You can multiply or divide a Vector with a double using the operator * and /:
v2=2*v1; v3=v1/2;
Add and subtract vectors
v2+=v1; v3-=v1; v4=v1+v2; v5=v2-v3;
Cross and scalar product
v3=v1*v2; //Cross product double a=dot(v1,v2)//Scalar product
Resetting
You can reset the values of a vector to zero:
SetToZero(v1);
Comparing vectors
Element by element comparison with or without user-defined accuracy:v1==v2; v2!=v3; Equal(v3,v4,eps);//with accuracy eps
KDL::Rotation
A Rotation is the 3x3 matrix that represents the 3D rotation of an object wrt the reference frame.
<equation id="rotation">$ \textrm{KDL::Rotation} = \left[\begin{array}{ccc}Xx&Yx&Zx\\Xy&Yy&Zy\\Xz&Yz&Zz\end{array}\right] $<equation>
Creating Rotations
Safe ways to create a Rotation
The following result always in consistent Rotations. This means the rows/columns are always normalized and orthogonal:
Rotation r1; //The default constructor, initializes to an 3x3 identity matrix Rotation r1 = Rotation::Identity();//Identity Rotation = zero rotation Rotation r2 = Rotation::RPY(roll,pitch,yaw); //Rotation built from Roll-Pitch-Yaw angles Rotation r3 = Rotation::EulerZYZ(alpha,beta,gamma); //Rotation built from Euler Z-Y-Z angles Rotation r4 = Rotation::EulerZYX(alpha,beta,gamma); //Rotation built from Euler Z-Y-X angles Rotation r5 = Rotation::Rot(vector,angle); //Rotation built from an equivalent axis(vector) and an angle.
Other ways
The following should be used with care, they can result in inconsistent rotation matrices, since there is no checking if columns/rows are normalized or orthogonal
Rotation r6( Xx,Yx,Zx,Xy,Yy,Zy,Xz,Yz,Zz);//Give each individual element (Column-Major) Rotation r7(vectorX,vectorY,vectorZ);//Give each individual column
Getting values
Individual values, the indices go from 0..2:
double Zx = r1(0,2);
r1.GetEulerZYZ(alpha,beta,gamma); r1.GetEulerZYX(alpha,beta,gamma); r1.GetRPY(roll,pitch,yaw); axis = r1.GetRot();//gives only rotation axis angle = r1.GetRotAngle(axis);//gives both angle and rotation axis
vecX=r1.UnitX();//or r1.UnitX(vecX); vecY=r1.UnitY();//or r1.UnitY(vecY); vecZ=r1.UnitZ();//or r1.UnitZ(vecZ);
Inverting Rotations
Replacing a rotation by its inverse:
r1.SetInverse();//r1 is inverted and overwritten
r2=r1.Inverse();//r2 is the inverse rotation of r1
Composing rotations
Compose two rotations to a new rotation, the order of the rotations is important:
r3=r1*r2;
r1.DoRotX(angle); r2.DoRotY(angle); r3.DoRotZ(angle);
r1 = r1*Rotation::RotX(angle)
Rotation of a Vector
Rotating a Vector using a Rotation and the operator *:v2=r1*v1;
Comparing Rotations
Element by element comparison with or without user-defined accuracy:r1==r2; r1!=r2; Equal(r1,r2,eps);
KDL::Frame
A Frame is the 4x4 matrix that represents the pose of an object/frame wrt a reference frame. It contains:
- a Rotation M for the rotation of the object/frame wrt the reference frame.
- a Vector p for the position of the origin of the object/frame in the reference frame
<equation id="frame">$ \textrm{KDL::Frame} = \left[\begin{array}{cc}\mathbf{M}(3 \times 3) &p(3 \times 1)\\ 0(1 \times 3)&1 \end{array}\right] $<equation>
Creating Frames
Frame f1;//Creates Identity frame Frame f1=Frame::Identity();//Creates an identity frame: Rotation::Identity() and Vector::Zero() Frame f2(your_rotation);//Create a frame with your_rotation and a zero vector Frame f3(your_vector);//Create a frame with your_vector and a identity rotation Frame f4(your_rotation,your_vector);//Create a frame with your_rotation Frame f5(your_vector,your_rotation);//and your_vector Frame f5(f6);//the copy constructor
Getting values
Individual values from the 4x4 matrix, the indices go from 0..3:double x = f1(0,3); double Yy = f1(1,1);
Vector p = f1.p; Rotation M = f1.M;
Composing frames
You can use the operator * to compose frames. If you have a Frame F_A_B that expresses the pose of frame B wrt frame A, and a Frame F_B_C that expresses the pose of frame C wrt to frame B, the calculation of Frame F_A_C that expresses the pose of frame C wrt to frame A is as follows:Frame F_A_C = F_A_B * F_B_C;
Inverting Frames
Replacing a frame by its inverse:
//not yet implementedf2=f1.Inverse();//f2 is the inverse of f1
Comparing frames
Element by element comparison with or without user-defined accuracy:f1==f2; f1!=f2; Equal(f1,f2,eps);
KDL::Twist
link to API documentationA Twist is the 6x1 matrix that represents the velocity of a Frame using a 3D translational velocity Vector vel and a 3D angular velocity Vector rot:
<equation id="twist">$\textrm{KDL::Twist} = \left[\begin{array}{c} v_x\\v_y\\v_z\\ \hline \omega_x \\ \omega_y \\ \omega_z \end{array} \right] = \left[\begin{array}{c} \textrm{vel} \\ \hline \textrm{rot}\end{array} \right] $<equation>
Creating Twists
Twist t1; //Default constructor, initializes both vel and rot to Zero Twist t2(vel,rot);//Vector vel, and Vector rot Twist t3 = Twist::Zero();//Zero twist
Getting values
Using the operators [ ] and ( ), the indices from 0..2 return the elements of vel, the indices from 3..5 return the elements of rot:
double vx = t1(0); double omega_y = t1[4]; t1(1) = vy; t1[5] = omega_z;
double vx = t1.vel.x();//or vx = t1.vel(0); double omega_y = t1.rot.y();//or omega_y = t1.rot(1); t1.vel.y(v_y);//or t1.vel(1)=v_y; //etc
Multiply/Divide with a scalar
The same operators as for Vector are available:t2=2*t1; t2=t1*2; t2=t1/2;
Adding/subtracting Twists
The same operators as for Vector are available:t1+=t2; t1-=t2; t3=t1+t2; t3=t1-t2;
Comparing Twists
Element by element comparison with or without user-defined accuracy:t1==t2; t1!=t2; Equal(t1,t2,eps);
KDL::Wrench
A Wrench is the 6x1 matrix that represents a force on a Frame using a 3D translational force Vector force and a 3D moment Vector torque:
<equation id="wrench">$\textrm{KDL::Wrench} = \left[\begin{array}{c} f_x\\f_y\\f_z\\ \hline t_x \\ t_y \\ t_z \end{array} \right] = \left[\begin{array}{c} \textrm{force} \\ \hline \textrm{torque}\end{array} \right] $<equation>
Creating Wrenches
Wrench w1; //Default constructor, initializes force and torque to Zero Wrench w2(force,torque);//Vector force, and Vector torque Wrench w3 = Wrench::Zero();//Zero wrench
Getting values
Using the operators [ ] and ( ), the indices from 0..2 return the elements of force, the indices from 3..5 return the elements of torque:
double fx = w1(0); double ty = w1[4]; w1(1) = fy; w1[5] = tz;
double fx = w1.force.x();//or fx = w1.force(0); double ty = w1.torque.y();//or ty = w1.torque(1); w1.force.y(fy);//or w1.force(1)=fy;//etc
Multiply/Divide with a scalar
The same operators as for Vector are available:w2=2*w1; w2=w1*2; w2=w1/2;
Adding/subtracting Wrenchs
The same operators as for Twist are available:w1+=w2; w1-=w2; w3=w1+w2; w3=w1-w2;
Comparing Wrenchs
Element by element comparison with or without user-defined accuracy:w1==w2; w1!=w2; Equal(w1,w2,eps);
Twist and Wrench transformations
Wrenches and Twists are expressed in a certain reference frame; the translational Vector vel of the Twists and the moment Vector torque of the Wrenches represent the velocity of, resp. the moment on, a certain reference point in that frame. Common choices for the reference point are the origin of the reference frame or a task specific point.The values of a Wrench or Twist change if the reference frame or reference point is changed.
Changing only the reference point
If you want to change the reference point you need the Vector v_old_new from the old reference point to the new reference point expressed in the reference frame of the Wrench or Twist:t2 = t1.RefPoint(v_old_new); w2 = w1.RefPoint(v_old_new);
Changing only the reference frame
If you want to change the reference frame but want to keep the reference point intact you can use a Rotation matrix R_AB which expresses the rotation of the current reference frame B wrt to the new reference frame A:ta = R_AB*tb; wa = R_AB*wb;
Note: This operation seems to multiply a 3x3 matrix R_AB with 6x1 matrices tb or wb, while in reality it uses the 6x6 Screw transformation matrix derived from R_AB.
Changing both the reference frame and the reference point
If you want to change both the reference frame and the reference point you can use a Frame F_AB which contains (i) Rotation matrix R_AB which expresses the rotation of the current reference frame B wrt to the new reference frame A and (ii) the Vector v_old_new from the old reference point to the new reference point expressed in A:ta = F_AB*tb; wa = F_AB*wb;
Note: This operation seems to multiply a 4x4 matrix F_AB with 6x1 matrices tb or wb, while in reality it uses the 6x6 Screw transformation matrix derived from F_AB.
First order differentiation and integration
t = diff(F_w_A,F_w_B,timestep)//differentiation F_w_B = F_w_A.addDelta(t,timestep)//integration
Kinematic Trees
A KDL::Chain or KDL::Tree composes/consists of the concatenation of KDL::Segments. A KDL::Segment composes a KDL::Joint and KDL::RigidBodyInertia, and defines a reference and tip frame on the segment. The following figures show a KDL::Segment, KDL::Chain, and KDL::Tree, respectively. At the bottom of this page you'll find the links to a more detailed description.
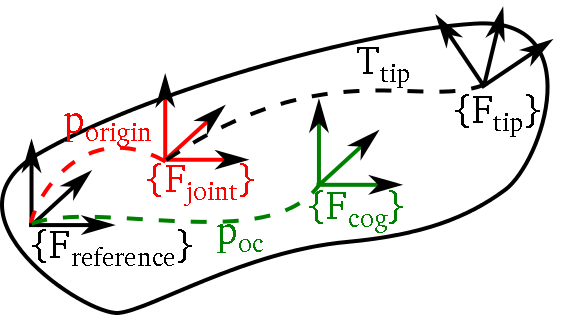 KDL segment
KDL segment
- Black: KDL::Segment:
- reference frame {F_reference} (implicitly defined by the definition of the other frames wrt. this frame)
- tip frame {F_tip}: frame from the end of the joint to the tip of the segment, default: Frame::Identity(). The transformation from the joint to the tip is denoted T_tip (in KDL directly represented by a KDL::Frame). In a kinematic chain or tree, a child segment is added to the parent segment's tip frame (tip frame of parent=reference frame of the child(ren)).
- composes a KDL::Joint (red) and a KDL::RigidBodyInertia (green)
- Red: KDL::Joint: single DOF joint around or along an axis of the joint frame {F_joint}. This joint frame has the same orientation as the the reference frame {F_reference} but can be offset wrt. this reference frame by the vector p_origin (default: no offset).
- Green: KDL::RigidBodyInertia: Cartesian space inertia matrix, the arguments are the mass, the vector from the reference frame {F_reference} to cog (p_cog) and the rotational inertia in the cog frame {F_cog}.
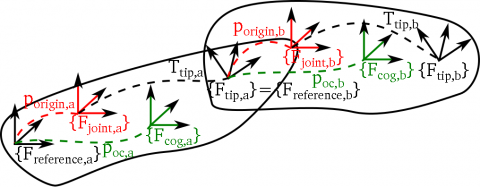 KDL chain
KDL chain 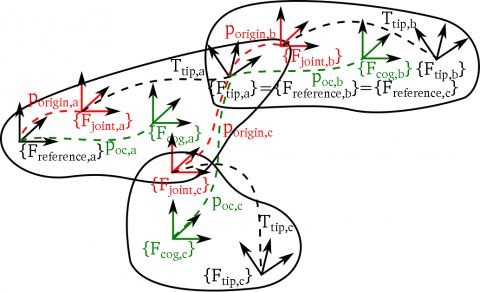 KDL tree
KDL tree
Select your revision: (1.0.x is the released version, 1.1.x is under discussion (see kinfam_refactored git branch))
Kinematic Trees - KDL 1.0.x
KDL::Joint
Link to APIA Joint allows translation or rotation in one degree of freedom between two Segments
Creating Joints
Joint rx = Joint(Joint::RotX);//Rotational Joint about X Joint ry = Joint(Joint::RotY);//Rotational Joint about Y Joint rz = Joint(Joint::RotZ);//Rotational Joint about Z Joint tx = Joint(Joint::TransX);//Translational Joint along X Joint ty = Joint(Joint::TransY);//Translational Joint along Y Joint tz = Joint(Joint::TransZ);//Translational Joint along Z Joint fixed = Joint(Joint::None);//Rigid Connection
Pose and twist of a Joint
Joint rx = Joint(Joint::RotX); double q = M_PI/4;//Joint position Frame f = rx.pose(q); double qdot = 0.1;//Joint velocity Twist t = rx.twist(qdot);
KDL::Segment
Link to APIA Segment is an ideal rigid body to which one single Joint is connected and one single tip frame. It contains:
- a Joint located at the root frame of the Segment.
- a Frame describing the pose between the end of the Joint and the tip frame of the Segment.
Creating Segments
Segment s = Segment(Joint(Joint::RotX), Frame(Rotation::RPY(0.0,M_PI/4,0.0), Vector(0.1,0.2,0.3) ) );
Pose and twist of a Segment
double q=M_PI/2;//joint position Frame f = s.pose(q);//s constructed as in previous example double qdot=0.1;//joint velocity Twist t = s.twist(q,qdot);
KDL::Chain
Link to APIA KDL::Chain is
- a kinematic description of a serial chain of bodies connected by joints.
- built out of KDL::Segments.
A Chain has
- a default constructor, creating an empty chain without any segments.
- a copy-constructor, creating a copy of an existing chain.
- a =-operator.
Chain chain1; Chain chain2(chain3); Chain chain4 = chain5;
Chains are constructed by adding segments or existing chains to the end of the chain. These functions add copies of the arguments, not the arguments themselves!
chain1.addSegment(segment1); chain1.addChain(chain2);
You can get the number of joints and number of segments (this is not always the same since a segment can have a Joint::None, which is not included in the number of joints):
unsigned int nj = chain1.getNrOfJoints(); unsigned int js = chain1.getNrOfSegments();
You can iterate over the segments of a chain by getting a reference to each successive segment:
Segment& segment3 = chain1.getSegment(3);
KDL::Tree
Link to APIA KDL::Tree is
- a kinematic description of a tree of bodies connected by joints.
- built out of KDL::Segments.
A Tree has
- a constructor that creates an empty tree without any segments and with the given name as its root name. The root name will be "root" if no name is given.
- a copy-constructor, creating a copy of an existing tree.
- a =-operator
Tree tree1; Tree tree2("RootName"); Tree tree3(tree4); Tree tree5 = tree6;
Trees are constructed by adding segments, existing chains or existing trees to a given hook name. The methods will return false if the given hook name is not in the tree. These functions add copies of the arguments, not the arguments themselves!
bool exit_value; exit_value = tree1.addSegment(segment1,"root"); exit_value = tree1.addChain(chain1,"Segment 1"); exit_value = tree1.addTree(tree2,"root");
You can get the number of joints and number of segments (this is not always the same since a segment can have a fixed joint (Joint::None), which is not included in the number of joints):
unsigned int nj = tree1.getNrOfJoints(); unsigned int js = tree1.getNrOfSegments();
You can retrieve the root segment:
std::map<std::string,TreeElement>::const_iterator root = tree1.getRootSegment();
You can also retrieve a specific segment in a tree by its name:
std::map<std::string,TreeElement>::const_iterator segment3 = tree1.getSegment("Segment 3");
You can retrieve the segments in the tree:
std::map<std::string,TreeElement>& segments = tree1.getSegments();
It is possible to request the chain in a tree between a certain root and a tip:
bool exit_value; Chain chain; exit_value = tree1.getChain("Segment 1","Segment 3",chain); //Segment 1 and segment 3 are included but segment 1 is renamed. Chain chain2; exit_value = tree1.getChain("Segment 3","Segment 1",chain2); //Segment 1 and segment 3 are included but segment 3 is renamed.
Kinematic Trees - KDL 1.1.x
KDL::Joint
Link to APIA Joint allows translation or rotation in one degree of freedom between two Segments
Creating Joints
Joint rx = Joint(Joint::RotX);//Rotational Joint about X Joint ry = Joint(Joint::RotY);//Rotational Joint about Y Joint rz = Joint(Joint::RotZ);//Rotational Joint about Z Joint tx = Joint(Joint::TransX);//Translational Joint along X Joint ty = Joint(Joint::TransY);//Translational Joint along Y Joint tz = Joint(Joint::TransZ);//Translational Joint along Z Joint fixed = Joint(Joint::None);//Rigid Connection
Pose and twist of a Joint
Joint rx = Joint(Joint::RotX); double q = M_PI/4;//Joint position Frame f = rx.pose(q); double qdot = 0.1;//Joint velocity Twist t = rx.twist(qdot);
KDL::Segment
Link to APIA Segment is an ideal rigid body to which one single Joint is connected and one single tip frame. It contains:
- a Joint located at the root frame of the Segment.
- a Frame describing the pose between the end of the Joint and the tip frame of the Segment.
Creating Segments
Segment s = Segment(Joint(Joint::RotX), Frame(Rotation::RPY(0.0,M_PI/4,0.0), Vector(0.1,0.2,0.3) ) );
Pose and twist of a Segment
double q=M_PI/2;//joint position Frame f = s.pose(q);//s constructed as in previous example double qdot=0.1;//joint velocity Twist t = s.twist(q,qdot);
KDL::Chain
Link to APIA KDL::Chain is
- a kinematic description of a serial chain of bodies connected by joints.
- built out of KDL::Segments.
A Chain has
- a default constructor, creating an empty chain without any segments.
- a copy-constructor, creating a copy of an existing chain.
- a =-operator is supported too.
Chain chain1; Chain chain2(chain3); Chain chain4 = chain5;
Chains are constructed by adding segments or existing chains to the end of the chain. All segments must have a different name (or "NoName"), otherwise the methods will return false and the segments will not be added. The functions add copies of the arguments, not the arguments themselves!
bool exit_value; bool exit_value = chain1.addSegment(segment1); exit_value = chain1.addChain(chain2);
You can get the number of joints and number of segments (this is not always the same since a segment can have a Joint::None, which is not included in the number of joints):
unsigned int nj = chain1.getNrOfJoints(); unsigned int js = chain1.getNrOfSegments();
You can iterate over the segments of a chain by getting a reference to each successive segment. The method will return false if the index is out of bounds.
Segment segment3; bool exit_value = chain1.getSegment(3, segment3);
You can also request a segment by name:
Segment segment3; bool exit_value = chain1.getSegment("Segment 3", segment3);
The root and leaf segment can be requested, as well as all segments in the chain.
bool exit_value; Segment root_segment; Segment leaf_segment; std::vector<Segment> segments; exit_value = chain1.getRootSegment(root_segment); exit_value = chain1.getLeafSegment(leaf_segment); exit_value = chain1.getSegments(segments);
You can request a part of the chain between a certain root and a tip:
bool exit_value; Chain part_chain; exit_value = chain1.getChain_Including(1,3, part_chain); exit_value = chain1.getChain_Including("Segment 1","Segment 3", part_chain); //Segment 1 and Segment 3 are included in the new chain! exit_value = chain1.getChain_Excluding(1,3, part_chain); exit_value = chain1.getChain_Excluding("Segment 1","Segment 3", part_chain); //Segment 1 is not included in the chain. Segment 3 is included in the chain.
There is a function to copy the chain up to a given segment number or segment name:
bool exit_value; Chain chain_copy; exit_value = chain1.copy(3, chain_copy); exit_value = chain1.copy("Segment 3", chain_copy); //Segment 3, 4,... are not included in the copy!
KDL::Tree
Link to APIA KDL::Tree is
- a kinematic description of a tree of bodies connected by joints.
- built out of KDL::Segments.
A Tree has
- a constructor that creates an empty tree without any segments and with the given name as its root name. The root name will be "root" if no name is given.
- a copy-constructor, creating a copy of an existing tree.
- a =-operator.
Tree tree1; Tree tree2("RootName"); Tree tree3(tree4); Tree tree5 = tree6;
Trees are constructed by adding segments, existing chains or existing trees to a given hook name. The methods will return false if the given hook name is not in the tree. These functions add copies of the arguments, not the arguments themselves!
bool exit_value; exit_value = tree1.addSegment(segment1,"root"); exit_value = tree1.addChain(chain1,"Segment 1"); exit_value = tree1.addTree(tree2,"root");
You can get the number of joints and number of segments (this is not always the same since a segment can have a Joint::None, which is not included in the number of joints):
unsigned int nj = tree1.getNrOfJoints(); unsigned int js = tree1.getNrOfSegments();
You can retrieve the root segment and the leaf segments:
bool exit_value; std::map<std::string,TreeElement>::const_iterator root; std::map<std::string,TreeElement> leafs; exit_value = tree1.getRootSegment(root); exit_value = tree1.getLeafSegments(leafs);
You can also retrieve a specific segment in a tree by its name:
std::map<std::string,TreeElement>::const_iterator segment3; bool exit_value = tree1.getSegment("Segment 3",segment3);
You can retrieve the segments in the tree:
std::map<std::string,TreeElement> segments; bool exit_value = tree1.getSegments(segments);
It is possible to request the chain in a tree between a certain root and a tip:
bool exit_value; Chain chain; exit_value = tree1.getChain("Segment 1","Segment 3",chain); //Segment 1 and segment 3 are included but segment 1 is renamed. Chain chain2; exit_value = tree1.getChain("Segment 3","Segment 1",chain2); //Segment 1 and segment 3 are included but segment 3 is renamed.
This chain can also be requested in a tree structure with the given root name ("root" if no name is given).
bool exit_value; Tree tree; exit_value = tree1.getChain("Segment 1","Segment 3",tree,"RootName"); Tree tree2; exit_value = tree1.getChain("Segment 3","Segment 1",tree2,"RootName");
There is a function to copy a tree excluding some segments and all their decendants.
bool exit_value; Tree tree_copy; exit_value = tree1.copy("Segment 3", tree_copy); //tree1 is copied up to segment 3 (excluding segment 3). std::vector<std::string> vect; vect.push_back("Segment 1"); vect.push_back("Segment 7"); exit_value = tree1.copy(vect,tree_copy);
Kinematic and Dynamic Solvers
KDL contains for the moment only generic solvers for kinematic chains. They can be used (with care) for every KDL::Chain.
The idea behind the generic solvers is to have a uniform API. We do this by inheriting from the abstract classes for each type of solver:
- ChainFkSolverPos
- ChainFkSolverVel
- ChainIkSolverVel
- ChainIkSolverPos
A seperate solver has to be created for each chain. At construction time, it will allocate all necessary resources.
A specific type of solver can add some solver-specific functions/parameters to the interface, but still has to use the generic interface for it's main solving purpose.
The forward kinematics use the function JntToCart(...) to calculate the Cartesian space values from the Joint space values. The inverse kinematics use the function CartToJnt(...) to calculate the Joint space values from the Cartesian space values.
Recursive forward kinematic solvers
For now we only have one generic forward and velocity position kinematics solver.It recursively adds the poses/velocity of the successive segments, going from the first to the last segment, you can also get intermediate results by giving a Segment number:
ChainFkSolverPos_recursive fksolver(chain1); JntArray q(chain1.getNrOfJoints); q=... Frame F_result; fksolver.JntToCart(q,F_result,segment_nr);